에라토스테네스의 체로 풀면 좋은 문제라고 생각합니다.관련된 연산 이에 대해 잘 모르시는 분은 아래 에라토스테네스의 체에 대한 설명을 읽어보시기 바랍니다.
02/21/2023 – (JAVA 연구) – (JAVA) 에라토스테네스의 체: 소수
(JAVA) 에라토스테네스의 체: 소수
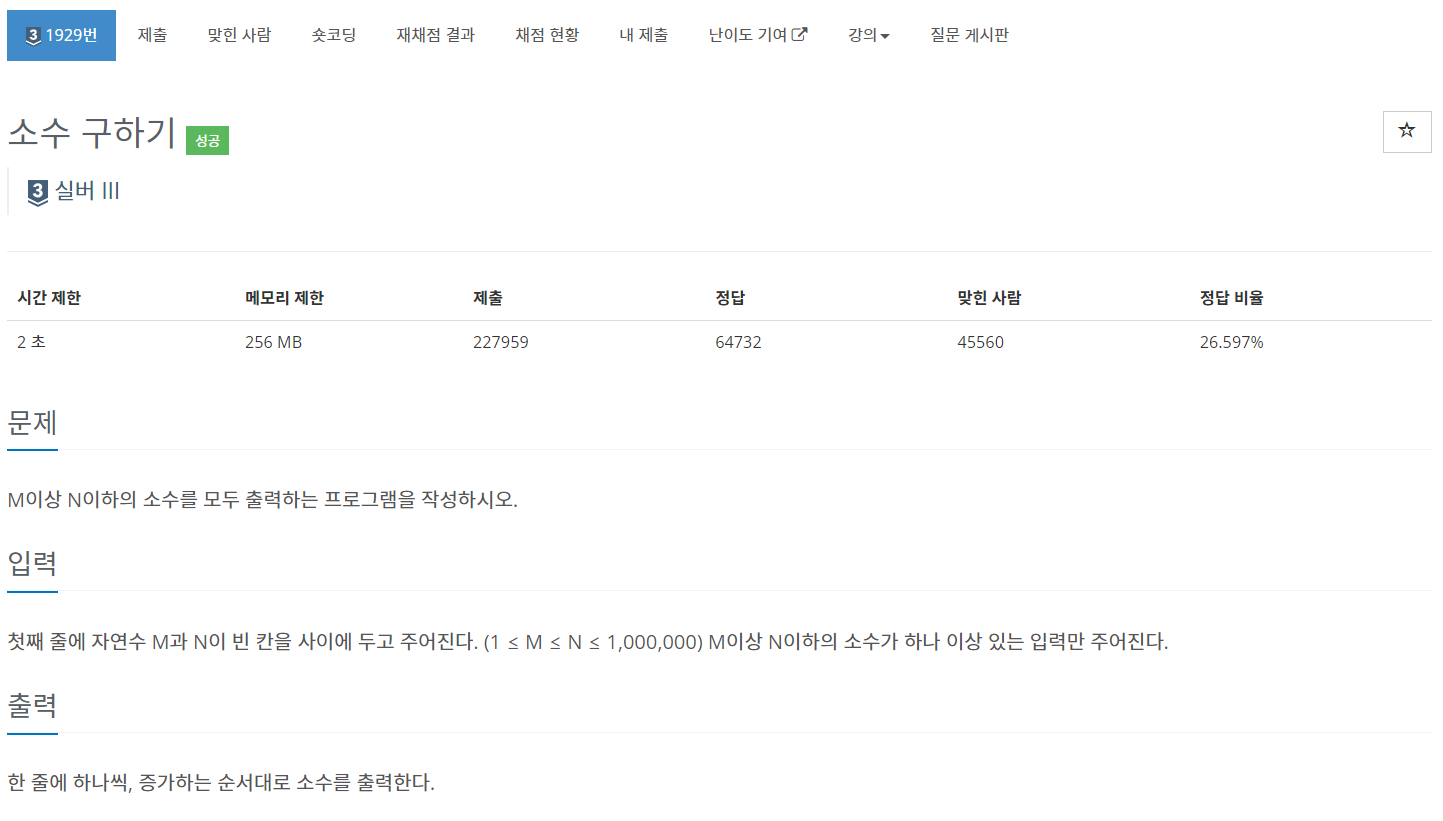
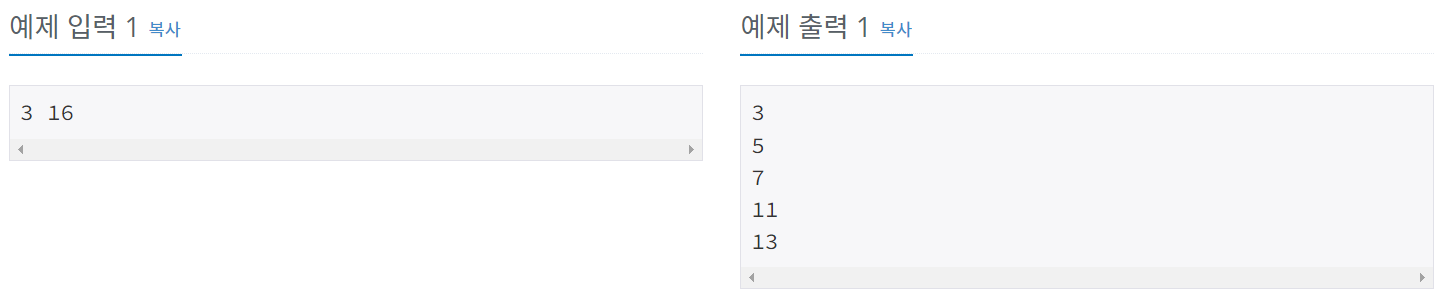
프라임이란 무엇입니까? 1보다 큰 자연수 중에서 1과 자기 자신만을 약수로 가지는 수, 에라토스테네스의 체란? 임의의 자연수 n에 대해 체처럼 걸러내기 때문에 이름이 지정된 이 알고리즘은
ddue5e5.tistory.com
이행 절차
1. 자연수 n의 범위만큼 큰 배열을 할당합니다.
2. 2부터 시작하여 주어진 숫자의 배수인 자신 이외의 모든 숫자에 줄을 긋습니다. (부울 true 처리)
3. 범위 내의 배열 값이 거짓인 값을 반환합니다.
코드 작성
import java.util.Scanner;
public class bj1929 {
public static boolean() arr;
public static void main(String() args) {
Scanner scanner = new Scanner(System.in);
int M = scanner.nextInt();
int N = scanner.nextInt();
arr = new boolean(N+1);
prime(); // 호출
for(int i=M; i<=N; i++) {
if(!arr(i)) { // false인 것만 출력
System.out.println(i);
}
}
}
// 에라토스테네스의 체 알고리즘
public static void prime() {
arr(0) = arr(1) = true;
for(int i=2; i<=Math.sqrt(arr.length); i++) {
if(!arr(i)) {
for(int j=i*i; j<arr.length; j+=i) {
arr(j) = true; // 소수가 아니다
}
}
}
}
}
정답 | 32728KB | 1020ms

정리하다
에라토스테네스의 체 알고리즘을 제대로 알고 있는지 확인하는 근본적인 문제라고 생각합니다.